How To Find True Count In Blackjack
True Count Method in Blackjack
- How To Find True Count In Blackjack Card Game
- How To Find True Count In Blackjack Game
- How To Find The True Count In Blackjack
- How To Find True Count In Blackjack Games
Up until now, we have discussed the cumulative count of all the cards that have been played, which is known as the running count. As you might already realize, a certain running count towards the beginning of a round is not worth as much as the same as it is towards the end. For example, if you were playing http://casinoslots-sa.co.za/skrill a six-deck shoe and had a running count of +5 after seeing 1 deck, you could estimate that the remaining 5 decks contain slightly more than the average amount of tens and aces. The extra good cards are spread out among the last 5 decks. On the other hand, if you were playing the same six-deck shoe and had a running count of +5 after seeing 5 decks, you could estimate that the last deck contains much more than the average amount of tens and aces. The extra good cards are highly concentrated in the last 52 cards.
2 all you need to know is that you hit until the TC is at or above +3. Presumably the reason for that is simulations show that two things happen as the count increases, a) your likelihood of busting increases, and b) the dealer’s likelihood of busting increases. Card counting is an advantage-play method that helps you determine when the blackjack odds are in your favor. It involves tracking cards as they come out of the shoe and assigning them point values. The running count helps you figure out when the shoe is rich in aces and 10-value cards.
True Count
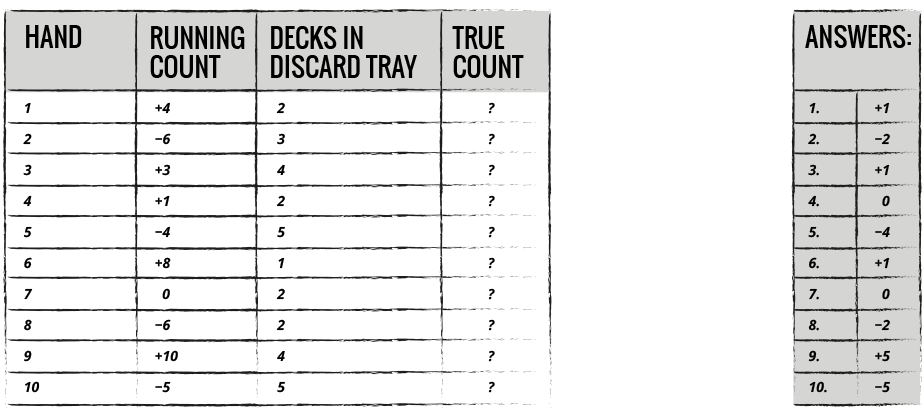
A balanced card counting method such as the popular Hi/Lo values a complete 52 card deck as zero. When you use a balanced counting system, you keep a running count of the cards as they are played, but you then have to divide running count by the number of decks not yet played to get the true count. If you are using Stanford Wong’s Hi-Lo Count from his book, Professional Blackjack, then each true count (or count-per-deck) is equal to a 0.5% change in your advantage. With a higher level count such as Wong’s Halves Count, Revere’s Point Count, or Uston’s APC, each count-per-deck is equal to (approximately) a 0.3% change in your. Once you find yourself at the end of the deck, if correct, your count should be no other but zero. You may hold the deck face down and count every single card, as it is turned over. Another way is to hold the deck face up and count every single card, as you progress through the deck.
A method of approximating our actual advantage is required for betting and play variation. The most popular method is to use the count per deck method, which is called the true count. To calculate it, the running count is divided into the number of decks that have not been seen. In the first example above, a running count of +5 with 5 decks remaining gives you a count per deck of +1. In the second example, a running count of +5 with 1 deck remaining gives you a count per deck of +5. The remaining cards in the second example are much better than the first. Therefore, you should always calculate the true count before making betting or playing decisions.
Some systems use different methods of making the calculations. As an example, you can divide your running count by the number of half decks remaining. For example, if you have a running count of -4 with 2 decks remaining, your count per half deck would be -1 since there are 4 half decks that you have not seen.
I have found that it is easier to calculate the count per deck rather than “per half deck”. As a result, the numbers for bet variation and insurance quoted in this guide are based on a count per deck.
Battle of the Babies: A Comparison of the Red 7, Hi-Lo, and KO Card Counting Systems
By Arnold Snyder(From Blackjack Forum Volume XIX #3, Fall 1999)
© Blackjack Forum 1999
[Editor's note: This is a technical article on how to best evaluate card counting systems. It addresses how system sellers sometimes fudge results to make their systems look better.
If you are new to card-counting, I recommend you start by reading Intro to Winning Blackjack and Card Counting: How It Works, Why It Works. For more information on card counting and blackjack basic strategy, and instructions for the Red 7 card counting system, see the end of this article.]
The Search for the 'Best' Card Counting System
New playerstypically search anxiously for the “best card counting system” beforelearning their first count. This article will provide simulation data on the RedSeven Count for comparison to the Hi-Lo and KO counts. Itwill also discuss important issues in the comparison of different blackjack cardcounting systems.
John Austonused the approach that has recently become commonly known as “score” to comparethe Red Seven (Red 7), Hi-Lo, and KO count systems. For those unfamiliar withthis approach, I would describe it very briefly as an attempt to comparesystems and games on an even playing field, assuming we define “even” as anequal and constant risk of ruin, assuming the same starting bankroll and thesame betting limits for each system in identical games.
In order to accomplish this in the sim, unrealistic bets are forced. For example, if the optimal bet is $137 with one system, but $138 with another, and $134 with a third system, then these are the bets that are placed. In practice, if these were human players and even if they had very accurately devised their count betting strategies to reflect a similar risk of ruin for identical $10,000 bankrolls, all would likely have bets of either $125 or $150—some slightly underbetting their banks, some slightly overbetting.
I canalready see a barrage of letters from players asking me to explain why anyonewould want an analysis based on such an impractical, nay impossible, bettingmethodology. Briefly, the purpose of this type of analysis is not to tell usour win rate to the exact penny per hour, nor is it to suggest that we shouldattempt to mimic the impractical betting strategies in the real world so thatwe may obtain optimal results.
The purposeis simply to evaluate the potential profitability of applying a system to agame assuming a given level of risk—one way of dealing with the “best cardcounting system” comparisons. Let me provide one practical example.
It is not difficult for me to set up a computer simulation where the Hi-Lo Count will outperform the Advanced Omega II (a much stronger and more difficult count), even when both counts are being played accurately and employing the same betting spread. All I have to do is play around with the betting strategies so that Omega II is waiting too long to put its big bets on the table. If I simply raise the true count by one or two numbers where these bigger bets are placed, then Hi-Lo will appear to be a stronger system. But in fact, the Hi-Lo is simply being played more aggressively and with a higher risk of ruin.
I firstlearned about this aggression factor back in the early 1980s, when I wasworking with Dr. John Gwynn, Jr. In order to compare different count systems usingthe same betting spread in the same game, I asked Gwynn to produce data showing thefull range of possible betting schemes for each system based on the varioustrue counts. For example, with the Hi-Lo Count, spreading from 1-2-4 units in asingle-deck game, he would produce data showing the bet raises to 2 and then 4units at +1 and +2, then +1 and +3, then +2 and +3, then +2 and +4, etc.
The dataGwynn and I came up with showed nothing about risk of ruin, but it did showthat a player who wanted to optimize his percent advantage over the house coulddo so by raising his bets at precisely the right counts. A player who wanted tooptimize his dollar return, on the other hand, could do so by betting moreaggressively (placing high bets earlier), even though this tactic would lowerhis percentage return.
Whenever Ipublished Gwynn’s system comparison data, I always chose the betting schemethat would provide the highest percent advantage to the player. I did thisbecause it was more realistic. A player with an unlimited bankroll, in fact,will show the highest dollar return if he places his high bet as soon as he haseven the slightest fraction of a percent advantage over the house. Players withunlimited bankrolls, however, do not exist. Such hypothetical players have norisk of ruin because they can always dig out more money.
In the realworld, it is more meaningful to optimize the percent advantage than the maximumpotential dollar win. In optimizing the percent advantage from Gwynn’s data formany systems in various games back in the early to mid-80s, and then up intothe mid-90s using John Imming’s RWC software, I discovered that the optimalbetting spreads were never intuitive. If I was spreading from 1-2-4-8 units ina 6-deck game, one system might perform best by raising bets at +1, +2, +4, and+5; while another’s optimal betting scheme would raise at +2, +4, +5 and +6;while yet another might perform best at +1, +3, +4 and +6.
When Ididn’t examine every possible betting scheme for each system, I would often seedata that would seem illogical. A system with a lower betting correlation andplaying efficiency would appear to outperform a technically superior system. Inalmost all cases, as soon as I would look at the results of the optimal bettingscheme for that system, defining optimal as the scheme that would produce thegreatest percent advantage, the greater profit potential of a technicallysuperior system would exhibit itself.
Optimizingsystem performance to obtain the highest percent advantage for each system doesnot ensure that all systems being so compared are playing with the same levelof risk. This was simply the best way I knew to compare the various systems’ultimate levels of performance.
Misleading Simulation Data for the KO Count
One of theworst examples of misleading simulation data from ill-chosen betting schemescan be found in Knock-Out Blackjack by Olaf Vancura and Ken Fuchs. Theydesigned a unique method of attempting to simulate equivalent levels of risk intheir system comparisons that produced data that computer programmers used torefer to as GIGO—garbage in, garbage out. The system comparison charts inChapter Five of the 1996 edition and again in the Appendix of the 1998 editionwould lead one to believe that the KO Count was superior to or equal to justabout every other counting system on the planet, and especially powerful inone-deck games.
Forexample, the chart below reproduces the simulation data provided by Knock-OutBlackjack comparing the win rates for KO vs. Red 7, Hi-Lo, and Omega II,assuming 1-5 spreads in the one and two-deck games, 1-8 in the 6-deck games,and 1-10 in the 8-deck games, with all systems using the 16 most importantstrategy indices.
The Simulation Data Provided by Knock-Out Blackjack
| 1-deck | 2-deck | 6-deck | 8-deck | |
| KO | 1.53 | 1.11 | 0.62 | 0.52 |
| Red7 | 1.46 | 1.08 | 0.61 | 0.50 |
| Hi-Lo | 1.47 | 1.08 | 0.61 | 0.52 |
| Omega | 1.52 | 1.15 | 0.68 | 0.57 |
When Ifirst looked at this data back in 1996, my initial thought was, “Impossible! KObeating Omega II in a single-deck game? And beating Hi-Lo in all games?” I didnot know whether or not it might beat Red Seven, but it was illogical to methat it would perform so powerfully, so consistently, in comparison with thebalanced counts. I knew that Red Seven performed close to Hi-Lo in shoe games,and did occasionally outperform it, but never in single deck.
I ran somesingle-deck simulations myself using John Imming’s software, setting up thegame and system conditions as described by Vancura and Fuchs, and quicklyconfirmed what I already knew—that KO was similar to Red Seven in performance,but notably less profitable than Hi-Lo and Omega II. In fact, it also slightlyunder-performed Red Seven throughout all the tests I ran.
I calledAnthony Curtis, who was distributing the KO book through Huntington Press (nowpublisher of the second edition) and told Curtis that I thought the authors mayhave jerry-rigged the sims to make KO appear stronger than it actually was. Itold him that in the one-deck sims I was running, Red Seven outperformed KO,not by much, but slightly.
Curtis assured me that he felt the authors were honest and that their simulation data was real, with no intention to skew the system comparison data. At this point, I had never met Olaf Vancura or Ken Fuchs, so I did not know if these guys were legitimate experts or big phonies. I have met and corresponded with both of them since, and I now know that, in fact, they are both gentlemen and scholars with no intent to deceive.
Here’swhere Vancura and Fuchs went wrong. KO’s imbalance makes it strongest and mostaccurate when the running count is at its pivot. So, the authors, verylogically, set up their sims so that KO was placing its high bets precisely atthis point. The other systems, however, were then forced in their simulationsto play with the same “average bet” that KO used.
The KOcounting system is actually very easy to use and very strong. It is similar instrength to the Red Seven, which itself is close to the Hi-Lo in strength withincertain confines. In fact, Hi-Lo is notably superior to both Red Seven andKO in one and two-deck games, and from many professional players’ perspectives,where accurate bet-sizing according to Kelly principles is important, Hi-Lo isalso far superior in shoe games.
For most casual players, however, I still believe the unbalanced counting systems are the best choice because they're simpler, can be played longer without costly errors, and allow the player to focus more on heat, getting away with a big bet spread, and other factors that matter more to your win rate than the count system you use.
I have been hesitant to publicly criticize Vancura’s and Fuch’s less than brilliant systemcomparisons in Knock Out Blackjack because the book really is one of thebetter ones on the market. The system is good. The explanations of blackjackand card counting are clear. There’s no get-rich-quick b.s., and I believethere was no intent to deceive.
I certainly don’t want to push new players away from Knock Out Blackjack and into the arms of one of the con-man books out there. Also, many serious players are already aware of why the KO system looks so strong in the sims Vancura and Fuchs provide in their book. There has been a lot of sim data posted on the various Internet blackjack sites that refute the findings in the KO book.
Also, anyone who looks at John Auston’s“World’s Greatest Blackjack Simulation” reports can see that KO’s strength is about what one would expect of a level one unbalanced counting system.
John Auston's Comparison of the Red 7, KO, Hi Lo and Omega II Card Counting Systems
In thechart below, I am reproducing John Auston’s “World’s Greatest BlackjackSimulation” data for comparing KO with Red Seven, Hi-Lo, and Omega II in thesame games that Vancura and Fuchs used in their book. The single-deckpenetration was 65% and all other games were 75%. Note that in the single anddouble deck games, Auston did not provide sim data for a 1-5 spread, so I usedhis data for 1-4 in single deck, and 1-6 in double.
Auston’s Data on KO, Red Seven, Hi-Lo, and Omega II
| 1-deck | 2-deck | 6-deck | 8-deck | |
| KO | 1.32 | 1.29 | 0.34 | 0.20 |
| Red7 | 1.34 | 1.24 | 0.44 | 0.39 |
| Hi-Lo | 1.38 | 1.30 | 0.34 | 0.26 |
| Omega | 1.64 | 1.54 | 0.51 | 0.56 |
Since theWorld’s Greatest Blackjack Simulation reports were published in 1997, manyplayers have asked me why the KO data does not show any indication of theconsistent superiority to other systems that KO is purported to exhibit in KnockOut Blackjack. The answer is simply that John Auston did not set up hisWGBJS sims so that all systems had to conform to the “average bet” specs of theoptimal KO betting strategy.
A few interesting points on Auston’s WGBJS data. Note that Omega II is in a class by itself, solidly trouncing the level one systems’ results in all games, as expected. Hi-Lo, KO and Red Seven go back and forth in their exhibitions of strength relative to each other.
Hi-Lo is slightly superior in single deck, while Red Seven and KO are about the same. Red Seven is slightly weaker in the double deck, where Hi-Lo and KO are about the same. Red Seven is stronger in both the six deck and eight deck, where Hi-Lo and KO are slightly weaker. If you actually look at all of the data in the WGBJS reports, you find that all three of these counts continually go back and forth, depending on the number of decks, penetration, and betting spreads. But none of them are a match for Advanced Omega II.
I wouldalso point out that even these independently run sims—done with no attempt tobias the data towards any system—are inadvertently set up with conditions thatare more favorable to the unbalanced counts, at least in comparison with theHi-Lo. This is because John Auston used the 'Illustrious 18' shoe strategy indicesfor all systems other than Advanced Omega II. These indices—which are the idealindices for shoe games—are not the best 18 indices for one and two deckgames. Since all but two of these indices call for Hi-Lo strategy changes atneutral to slightly positive counts (0 to +5), this is precisely the range ofcounts where both KO and Red Seven will perform best.
A Hi-Loplayer who is using more indices for the common playing variations that occurboth at negative counts and at higher positive counts would actually expect aperformance level closer to the Advanced Omega II system (which Auston simmedwith a full set of indices) in the one and two deck games. Red Seven and KOsimply do not have a playing accuracy level comparable to Hi-Lo outside thelimited Illustrious 18 range.
Also, RedSeven’s dominating performance in the six deck and eight deck games, where itsolidly trounces both Hi-Lo and KO, is due to the way the system is designed,where it performs with maximum strength when the advantage has risen by about1%. Because it is strongest at this point, this is where it will be placingmost high bets.
In these shoe games with only 75% penetration, higher advantages only rarely occur. So, Red Seven is optimized to play in precisely these types of games.
I can assure you, however, that it is playing with more risk than Hi-Lo, so in reality it would require a larger bankroll to play Red Seven to its optimum performance in these games. Auston’s six deck WGBJS data shows Red Seven’s average bet to be 1.63 units, while KO and Hi-Lo are making average bets of only 1.42 and 1.47 units respectively.
If we were to force average bets of 1.63 units on Hi-Lo and KO, they would perform even worse in comparison with Red Seven. KO’s playing and betting accuracy do not optimize until a 2% raise in the player advantage has occurred, and Hi-Lo suffers from not counting the sevens, which raises the Red Seven’s betting correlation (BC) and playing efficiency (PE) enough at its pivot point to justify the more frequent higher bets.
JohnAuston’s risk-adjusted analysis, which we have yet to look at in this article, solvesthe problem of equalizing the risk factors for the various systems tested, butit is still unfairly skewed toward the unbalanced systems in hand-held games,because it again uses only the Illustrious 18 range of indices, with which theunbalanced systems perform best.
One otherproblem with the Red Seven data is that in all of these sims—WGBJS andrisk-adjusted—the advanced version of the Red Seven system cannot be simulatedas published in the 1998 edition of Blackbelt in Blackjack [editor’snote: the Advanced Red Seven can now be simulated using CVDATA, which was notavailable at the time this article was written].
In shoe games, for example, I provide index numbers for the Advanced Red Seven that are to be used only in the second half of the shoe. The player is advised to use only the six “simple Red 7” indices in the first half of the shoe, then switch to the advanced indices for the second half. The ability to “step up” to the much more powerful Advanced Red Seven when ready is something not available to players with the KO Count.
Also,although both the simple and advanced Red Seven indices are employed by runningcount, the Advanced Red Seven advises the use of the “true edge” method ofestimating advantage for bet sizing, which is actually a simplified method ofadjusting to the true count. In other words, the Advanced Red Seven playerwould be making strategy plays by running count, but some of these plays wouldnot be made until after the 50% level of penetration was reached, while betsizing is done by true count.
The performance of Red Seven in these simulations will be hurt by not employing these techniques. The sims will simply not show accurate data for the Advanced Red Seven’s true power.
Also, theSBA software used for these simulations was incapable of counting sevens bycolor. John Auston adjusted for this deficiency by essentially counting all ofthe 7s as +1/2, instead of just the red sevens as +1. In both the 1983 and 1998editions of Blackbelt in Blackjack, I wrote: “One may even count allsevens as +1/2, or simply count every other seven as +1” in order to maintainthe same imbalance as is provided by counting just the red sevens—and over theyears not a few players have told me that this is what they do at the tables.'This method of unbalancing the count has a slightly better betting and playingefficiency than the traditional Red Seven, however. In prior sim comparisonspublished in Blackjack Forum, I always used Imming’s RWC software (no longercommercially available), which does allow counting by suit.
Also,Auston chose to simulate the Red Seven for his risk-adjusted analysis with theindices he derived from SBA, and which I published in the Red Seven Countedition of his “World’s Greatest Blackjack Simulation” report. So, both thebetting and playing strategies used in these risk-adjusted analyses aredifferent from those you will find in the 1998 (and 2005) edition of Blackbeltin Blackjack, which I believe to be superior. Just bear in mind that thesecomparisons are specifically for the 1997 version of the simple Red Seven aspublished in Auston’s WGBJ Sim.
More Problems With Comparing Card Counting Systems
Finally,the risk-adjusted method of analysis will give an unbalanced system an abilityto bet far more accurately in all games than would be possible in the realworld. A Hi-Lo or Omega II player who is using a true count system will trulyknow when his advantage is approximately +1/2%, +1%, +1.5%, +2%, etc., and hewill be able to size his bets accordingly. This would also be true of anAdvanced Red Seven player who is using the true edge method of bet sizing.
For a KO player or a simple Red Seven player who is purely going by the running count, an accurate bet can only be made at the pivot. If a Red Seven or KO running count is +6 above the pivot, the actual player advantage will be quite different in a six deck game if only two decks have been dealt than if 4.5 decks have been dealt.
This is whymost professional blackjack players steer clear of the unbalanced counts—andwhy I added the true edge methodology to the 1998 Advanced Red Seven. If youare betting multiple black chips for every ½% rise in your advantage, orcalling in a big player who will be doing this, you do not want to beconstantly overbetting and underbetting your optimal Kelly bet—or most likely,a fractional Kelly bet you’ve chosen to minimize your risk.
So, as youlook at this risk-adjusted comparison data, bear in mind all of these factors.The validity of the data extends as far as the assumptions used in the sims forplaying and betting. Ultimately, Red Seven and KO perform very well compared toHi-Lo, and I still believe these simplified unbalanced systems should be usedby most players for practical reasons, in particular the cost of errorsassociated with inaccurate true count adjustments.
Again, Iwant to emphasize that Hi-Lo is being severely penalized in the hand-held gamesin the charts below by using the Illustrious 18. If you use the Hi-Lo in one ortwo deck games and you are using the Illustrious 18 indices, then you couldprobably do almost as well with Red Seven or KO—better, if your true countadjustments aren’t perfect. Most single deck players I know use many moreindices than this in single deck, especially some negative indices that aremore important than some of the Illustrious 18 in these games, and unbalancedcounts are incapable of using more indices with accuracy.
Risk-Adjusted, One Deck, H17, DAS, 75% Dealt
| Spread | Hi-Lo | KO | Red Seven |
| 1-2 | 72.83 | 66.50 | 72.43 |
| 1-3 | 133.13 | 125.00 | 131.95 |
| 1-4 | 176.55 | 168.39 | 174.72 |
Risk-Adjusted, Two Deck, S17, DAS, 75% Dealt
| Spread | Hi-Lo | KO | Red Seven |
| 1-4 | 58.79 | 55.80 | 58.50 |
| 1-6 | 84.64 | 81.78 | 83.78 |
| 1-8 | 101.14 | 98.39 | 99.75 |
Risk-Adjusted, Six Deck, S17, DAS, LS, 75% Dealt
| Spread | Hi-Lo | KO | Red Seven |
| 1-8 | 24.71 | 22.74 | 26.39 |
| 1-10 | 29.43 | 27.36 | 30.99 |
| 1-12 | 32.91 | 30.85 | 34.53 |
Risk-Adjusted, Six Deck, S17, DAS, LS, 87.5% Dealt
| Spread | Hi-Lo | KO | Red Seven |
| 1-8 | 40.45 | 38.40 | 40.72 |
| 1-10 | 47.26 | 45.36 | 47.00 |
| 1-12 | 52.04 | 50.50 | 51.89 |
Risk-Adjusted, Six Deck, S17, DAS, LS, 92% Dealt
| Spread | Hi-Lo | KO | Red Seven |
| 1-8 | 73.74 | 71.54 | 68.24 |
| 1-10 | 85.26 | 82.83 | 77.57 |
| 1-12 | 93.62 | 91.07 | 84.46 |
In the sixdeck comparisons above, we have a perfect illustration of the power of thepivot. Note that with 4.5 decks dealt (75%), Red Seven is the strongestperformer. With five decks dealt, Hi-Lo and Red Seven pretty much equalize,both slightly outperforming KO. But look what happens when we go to 5.5 decksdealt out (91.67% penetration). Red Seven is now the weakest performer, as KOis capitalizing on its strength when many more opportunities arise for playingand betting with a 2% advantage.
The RedSeven (that is, the simple running count version tested here) simply performsbetter in shoes at most common levels of penetration, whereas KO performsbetter in the rare games with an extremely deep level.
Also, insome games under specific conditions, KO does outperform Hi-Lo in arisk-adjusted sim. For example, look at this six deck game with a lessfavorable set of rules:
Risk-Adjusted, Six Deck, H17, DAS, 75% Dealt
| Spread | Hi-Lo | KO | Red Seven |
| 1-8 | 6.60 | 6.66 | 6.30 |
| 1-10 | 9.20 | 9.95 | 9.83 |
| 1-12 | 11.90 | 12.54 | 12.10 |
Risk-Adjusted, Six Deck, H17, DAS, 87.5% Dealt
| Spread | Hi-Lo | KO | Red Seven |
| 1-8 | 15.03 | 15.10 | 15.13 |
| 1-10 | 19.69 | 19.82 | 19.50 |
| 1-12 | 23.43 | 23.74 | 22.94 |
KOoutperforms both Hi-Lo and Red Seven in these H17 games. Again, the explanationfor these types of seemingly aberrant results is that at some levels ofpenetration, and with certain rule sets, the sevens (which Hi-Lo ignores) areimportant enough on some of the Illustrious 18 strategy decisions as to givethese unbalanced counts, which count sevens, a slight edge. Also, the bettingschemes are such that the optimal high bets happen to occur very near theunbalanced counts’ pivots, and counting the sevens also gives them a slightlyhigher betting correlation right at this crucial point.
Unless weare adjusting an unbalanced count to a true count, we cannot cite its bettingcorrelation (BC) or playing efficiency (PE). For example, the Red Seven has abetting correlation of about 97% at the pivot, just slightly greaterthan the Hi-Lo. But the Hi-Lo has better than 96% betting correlation throughoutthe full range of counts that occur. It is simply incorrect to attempt tocompare a balanced system with an unbalanced system based on BC and PE ifyou are using the unbalanced system as a running count system.
Now let’slook at some 8-deck back-counting risk-adjusted comparisons (below). We’ll lookat the risk-adjusted results with six decks (75%), 6.5 decks (82%), and 7 decks(88%). Here again, we see that KO outperforms Red Seven at the very deepestlevel of penetration.
Risk-Adjusted, 8-Deck, Back Count S17, DAS, LS, 75% Dealt
| Spread | Hi-Lo | KO | Red Seven |
| 1-8 | 30.14 | 28.79 | 31.34 |
| 1-10 | 37.82 | 35.94 | 38.40 |
| 1-12 | 40.49 | 37.14 | 39.94 |
Risk-Adjusted, 8-Deck, Back Count S17, DAS, LS, 82% Dealt
| Spread | Hi-Lo | KO | Red Seven |
| 1-8 | 40.82 | 38.78 | 40.98 |
| 1-10 | 52.09 | 49.59 | 51.52 |
| 1-12 | 55.56 | 51.59 | 52.64 |
Risk-Adjusted, 8-Deck, Back Count S17, DAS, LS, 88% Dealt
| Spread | Hi-Lo | KO | Red Seven |
| 1-8 | 57.78 | 60.00 | 56.36 |
| 1-10 | 74.20 | 73.19 | 70.94 |
| 1-12 | 78.51 | 74.75 | 72.29 |
Note thatin most comparisons, regardless of the number of decks, Hi-Lo slightlyoutperforms both KO and Red Seven. I think in the real world, a good Hi-Loplayer would outperform the unbalanced running count players more than thesesim results indicate. In the hand-held games the Hi-Lo player would simply beable to use more strategy changes, and in the shoe games the Hi-Lo player wouldbe betting more accurately according to his advantage throughout the full rangeof counts that occur.
Overall, aswe would expect, the risk-adjusted comparisons do show Hi-Lo (accurately used)to be the stronger counting system.
For thoseof you who do not have John Auston’s “World’s Greatest Blackjack Simulation—RedSeven Edition,” I am reproducing below all of the running count indices thatJohn used in that report as well as in his risk-adjusted analyses. Note thatthese indices assume that you begin your count at 0. The indices werespecifically derived for the Red Seven Count that counts all sevens as +1/2instead of counting just the red sevens as +1. This would not change any of theindices.
Someplayers who use the Red Seven in this way have told me that the easiest way tocount by halves is to simply count every other seven as +1. I believe Iactually first heard of this technique being used by players who did it withWong’s Halves Count. I may even have read about the technique in one of Wong’snewsletters many years ago, or possibly in one of the earlier versions ofWong’s Professional Blackjack.
I was unable to find the reference in print but the technique has been used by some Red Seven and Halves players for many years. I do not believe my suggestion that Red Seven players might count in this way in the 1983 Blackbelt in Blackjack was the first reference to this technique in print. Those who use it swear it is the easiest and most accurate way to count with these systems.
I once ran some simulations using Imming’s RWC software to compare the difference between counting the red sevens as +1 and all sevens as +1/2, but the results were statistically insignificant. I suspect that I did not run a sufficient number of hands. (Computers were notably slower back then.) The simulations Auston used in his WGBG repots, his risk-adjusted analyses, and his truly amazing Blackjack Risk Manager software, are all based on sims of 400 million hands each, quite enough to obtain statistically significant data for practical comparisons.
Below, youwill find all of the Red Seven risk-adjusted data that John Auston produced forthis study. Some Red Seven players may regret that he did not run risk adjustedsims on the full range of rule sets that he did for Hi-Lo and KO.
John chose five different rule sets for his Red Seven single-deck analyses, and four different rule sets for each of the two deck, six deck and eight deck analyses. I don’t think a more exhaustive risk-adjusted analysis of this version of the Red Seven is called for at the present, as I believe that most Red Seven players probably use one of the versions (simple or advanced) from Blackbelt in Blackjack, rather than the version I published in the WGBJ sim report.
| The Red 7 Simulation Indices | ||||
| 8-Deck | 6-Deck | 2-Deck | 1-Deck | |
| Index/IRC | 0 | 0 | 0 | 0 |
| Insurance | +20 | +15 | +5 | +2 |
| 16 vs 9 | +25 | +21 | +7 | +4 |
| 16 vs 10 | +9 | +6 | +2 | +1 |
| 15 vs 10 | +22 | +17 | +6 | +3 |
| 13 vs 2 | +1 | +1 | +1 | +1 |
| 13 vs 3 | -5 | -4 | -1 | 0 |
| 12 vs 2 | +20 | +16 | +6 | +4 |
| 12 vs 3 | +15 | +11 | +5 | +3 |
| 12 vs 4 | +9 | +6 | +2 | +2 |
| 12 vs 5 | -2 | +1 | 0 | +1 |
| 12 vs 6 | 0/-10* | 0/-7 | +1/-2 | +1/-1 |
| 11 vs Ace | +13/+7 | +10/+4 | +2/-1 | 0/-1 |
| 10 vs 10 | +20 | +16 | +5 | +3 |
| 10 vs Ace | +20/+18 | +16/+13 | +5/+4 | +2 |
| 9 vs 2 | +11 | +9 | +3 | +2 |
| 9 vs 7 | +21 | +16 | +6 | +3 |
| 10,10 vs 5 | +24 | +19 | +7 | +4 |
| 10,10 vs 6 | +23 | +18 | +7 | +4 |
| Surrender | ||||
| 15 vs 9 | +17 | +14 | +5 | +3 |
| 15 vs 10 | +8 | +5 | +2 | +1 |
| 15 vs Ace | +15/+1 | +11/0 | +3/0 | +1/0 |
| 14 vs 10 | +18 | +14 | +5 | +3 |
| 1-Deck Special | ||||
| 8 vs 5 | N/A | N/A | N/A | +3 |
| 8 vs 6 | N/A | N/A | N/A | +3 |
| * Where two indices are shown, the first is for S17, the second for H17 | ||||
How To Find True Count In Blackjack Card Game
| Red 7 1-Deck ($Won/100) (exact indices, sim counted all 7s as .5, to simulate counting only red) | |||||
| S17 | S17DAS | H17 | H17DAS | H17D10 | |
| 26 | (1.15) | ||||
| 1-2 | 17.28 | 27.66 | 6.30 | 13.75 | 0.54 |
| 1-3 | 38.93 | 52.17 | 22.70 | 34.32 | 4.36 |
| 1-4 | 55.08 | 69.35 | 36.59 | 49.86 | 13.53 |
| 31 | (1.20) | ||||
| 1-2 | 41.89 | 56.37 | 23.87 | 36.61 | 5.38 |
| 1-3 | 77.33 | 94.65 | 54.47 | 71.01 | 23.56 |
| 1-4 | 103.50 | 122.07 | 78.70 | 96.26 | 42.62 |
| 35 | (1.20) | ||||
| 1-2 | 50.47 | 65.10 | 29.90 | 44.21 | 7.41 |
| 1-3 | 93.76 | 112.49 | 68.72 | 88.01 | 31.37 |
| 1-4 | 126.53 | 145.73 | 99.16 | 121.10 | 55.52 |
| 39 | (1.25) | ||||
| 1-2 | 81.98 | 99.37 | 55.24 | 72.43 | 22.40 |
| 1-3 | 143.75 | 164.25 | 111.00 | 131.95 | 63.09 |
| 1-4 | 187.64 | 207.98 | 152.38 | 174.72 | 97.81 |
| Red 7 2-Deck ($Won/100) (exact indices, sim counted all 7s as .5, to simulate counting only red) | |||||
| S17DAS | S17DASLS | H17DAS | H17DASLS | ||
| 52 | (0.95) | ||||
| 1-4 | 18.89 | 28.68 | 6.59 | 15.86 | |
| 1-6 | 29.69 | 42.69 | 17.33 | 28.63 | |
| 1-8 | 36.48 | 51.84 | 23.51 | 37.43 | |
| 62 | (0.95) | ||||
| 1-4 | 30.74 | 46.06 | 18.15 | 29.61 | |
| 1-6 | 45.45 | 66.48 | 32.13 | 48.54 | |
| 1-8 | 55.07 | 79.40 | 41.55 | 60.99 | |
| 70 | (1.00) | ||||
| 1-4 | 43.74 | 63.66 | 26.80 | 43.71 | |
| 1-6 | 63.38 | 90.70 | 44.75 | 68.54 | |
| 1-8 | 76.12 | 107.55 | 57.09 | 85.50 | |
| 78 | (1.00) | ||||
| 1-4 | 58.50 | 84.43 | 39.99 | 61.79 | |
| 1-6 | 83.78 | 119.19 | 64.06 | 95.05 | |
| 1-8 | 99.75 | 140.67 | 80.13 | 116.71 | |
| Red 7 6-Deck ($Won/100) (exact indices, sim counted all 7s as .5, to simulate counting only red) | |||||
| S17DAS | S17DASLS | H17DAS | H17DASLS | ||
| 4/6 | (0.90) | ||||
| 1-8 | 8.70 | 17.26 | 2.41 | 8.32 | |
| 1-10 | 10.83 | 20.67 | 4.54 | 11.32 | |
| 1-12 | 12.46 | 23.14 | 6.62 | 13.85 | |
| 4.5/6 | (0.95) | ||||
| 1-8 | 14.43 | 26.39 | 6.30 | 15.62 | |
| 1-10 | 17.80 | 30.99 | 9.83 | 19.96 | |
| 1-12 | 20.26 | 34.53 | 12.10 | 23.20 | |
| 5/6 | (0.95) | ||||
| 1-8 | 25.19 | 40.72 | 15.13 | 27.42 | |
| 1-10 | 29.81 | 47.00 | 19.50 | 33.61 | |
| 1-12 | 33.49 | 51.89 | 22.94 | 38.35 | |
| 5.5/6 | (0.95) | ||||
| 1-8 | 44.03 | 68.24 | 29.64 | 51.26 | |
| 1-10 | 50.94 | 77.57 | 36.33 | 60.70 | |
| 1-12 | 56.24 | 84.46 | 41.34 | 67.69 | |
| Red 7 6-Deck Back Count ($Won/100) Integer to rightof $ amount is Running Count of 1st bet (IRC=0) (exact indices, sim counted all 7s as .5, to simulate counting only red) | |||||
| S17DAS | S17DASLS | H17DAS | H17DASLS | ||
| 4/6 | (0.90) | ||||
| 1-1 | 21.32 (17) | 32.50 (14) | 18.29 (17) | 26.15 (17) | |
| 1-2 | 25.20 (14) | 38.00 (14) | 20.86 (14) | 30.63 (14) | |
| 1-4 | 26.59 (14) | 40.47 (11) | 22.43 (14) | 32.58 (14) | |
| 1-8 | 27.57 (11) | 41.60 (11) | 23.17 (14) | 33.79 (14) | |
| 1-12 | 27.77 (11) | 41.74 (11) | 23.31 (14) | 34.42 (11) | |
| 4.5/6 | (0.95) | ||||
| 1-1 | 31.34 (17) | 47.17 (17) | 26.03 (17) | 39.65 (17) | |
| 1-2 | 35.97 (14) | 53.93 (14) | 30.34 (17) | 45.07 (17) | |
| 1-4 | 38.07 (14) | 57.38 (14) | 32.43 (14) | 48.72 (14) | |
| 1-8 | 38.91 (11) | 58.85 (11) | 33.73 (14) | 49.75 (14) | |
| 1-12 | 39.69 (11) | 59.80 (11) | 33.52 (14) | 50.30 (14) | |
| 5/6 | (0.95) | ||||
| 1-1 | 46.55 (17) | 68.09 (17) | 40.32 (17) | 60.00 (17) | |
| 1-2 | 54.08 (14) | 76.25 (14) | 46.05 (17) | 67.21 (17) | |
| 1-4 | 58.12 (14) | 82.10 (14) | 49.61 (14) | 71.57 (14) | |
| 1-8 | 58.79 (14) | 83.85 (14) | 51.14 (14) | 73.84 (14) | |
| 1-12 | 59.50 (14) | 85.39 (11) | 51.08 (14) | 73.69 (14) | |
| 5.5/6 | (0.95) | ||||
| 1-1 | 73.47 (17) | 105.13 (17) | 65.39 (17) | 97.56 (17) | |
| 1-2 | 84.15 (14) | 117.91 (14) | 71.43 (17) | 106.00 (17) | |
| 1-4 | 90.14 (14) | 126.42 (14) | 77.30 (14) | 113.40 (14) | |
| 1-8 | 90.66 (14) | 126.28 (14) | 78.47 (14) | 115.95 (14) | |
| 1-12 | 90.88 (14) | 127.47 (14) | 78.44 (14) | 115.83 (14) | |
| Red 7 8-Deck ($Won/100) (exact indices, sim counted all 7s as .5, to simulate counting only red) | |||||
| S17DAS | S17DASLS | H17DAS | H17DASLS | ||
| 5.5/8 | (0.90) | ||||
| 1-8 | 4.03 | 9.80 | 0.22 | 3.19 | |
| 1-10 | 6.17 | 12.06 | 1.63 | 5.47 | |
| 1-12 | 7.56 | 14.28 | 2.93 | 7.47 | |
| 6/8 | (0.95) | ||||
| 1-8 | 7.30 | 14.78 | 1.79 | 7.24 | |
| 1-10 | 9.41 | 17.92 | 3.93 | 9.92 | |
| 1-12 | 11.68 | 20.46 | 5.72 | 12.61 | |
| 6.5/8 | (0.95) | ||||
| 1-8 | 11.71 | 21.27 | 4.54 | 12.51 | |
| 1-10 | 15.23 | 25.52 | 7.67 | 16.92 | |
| 1-12 | 17.70 | 28.72 | 9.88 | 20.04 | |
| 7/8 | (0.95) | ||||
| 1-8 | 18.85 | 32.32 | 10.09 | 21.61 | |
| 1-10 | 23.18 | 38.19 | 14.60 | 27.11 | |
| 1-12 | 26.46 | 42.44 | 17.82 | 31.28 | |
| Red 7 8-Deck Back Count ($Won/100) Integer to rightof $ amount is Running Count of 1st bet (IRC=0) (exact indices, sim counted all 7s as .5, to simulate counting only red) | |||||
| S17DAS | S17DASLS | H17DAS | H17DASLS | ||
| 5.5/8 | (0.90) | ||||
| 1-1 | 14.89 (17) | 23.29 (17) | 12.50 (17) | 18.52 (17) | |
| 1-2 | 17.52 (14) | 26.85 (14) | 14.29 (17) | 20.95 (17) | |
| 1-4 | 18.75 (14) | 28.49 (11) | 14.95 (14) | 22.75 (14) | |
| 1-8 | 19.19 (11) | 29.57 (11) | 15.63 (14) | 24.02 (14) | |
| 1-12 | 19.53 (11) | 29.97 (11) | 15.56 (14) | 23.82 (14) | |
| 6/8 | (0.95) | ||||
| 1-1 | 21.43 (17) | 31.34 (17) | 16.84 (17) | 25.68 (17) | |
| 1-2 | 23.85 (17) | 34.78 (14) | 18.85 (17) | 29.47 (17) | |
| 1-4 | 25.63 (14) | 38.40 (14) | 20.29 (14) | 32.28 (14) | |
| 1-8 | 26.54 (14) | 39.25 (11) | 20.72 (14) | 33.03 (14) | |
| 1-12 | 26.60 (11) | 39.94 (11) | 21.39 (14) | 33.10 (14) | |
| 6.5/8 | (0.95) | ||||
| 1-1 | 28.95 (17) | 40.98 (17) | 23.53 (17) | 36.36 (17) | |
| 1-2 | 32.99 (17) | 47.44 (17) | 27.10 (17) | 41.67 (17) | |
| 1-4 | 35.37 (14) | 51.52 (14) | 28.96 (14) | 44.36 (14) | |
| 1-8 | 36.80 (14) | 52.41 (14) | 29.93 (14) | 46.23 (14) | |
| 1-12 | 36.45 (14) | 52.64 (11) | 29.97 (14) | 46.46 (14) | |
| 7/8 | (0.95) | ||||
| 1-1 | 40.30 (17) | 56.36 (17) | 34.55 (20) | 50.00 (17) | |
| 1-2 | 46.51 (17) | 65.72 (17) | 40.22 (17) | 59.46 (17) | |
| 1-4 | 48.30 (14) | 70.94 (14) | 42.14 (17) | 61.91 (14) | |
| 1-8 | 49.76 (14) | 72.29 (14) | 43.55 (14) | 63.85 (14) | |
| 1-12 | 49.83 (14) | 72.29 (14) | 43.71 (14) | 64.20 (14) | |
How To Find True Count In Blackjack Game
For complete instructions on the Red 7 count, see The East Red 7 Count
How To Find The True Count In Blackjack
In summary, the 'best' blackjack card counting system for you, whether the Red Seven, Advanced Red Seven, KO, Hi-Lo, Zen, or some other count, will depend partly on your current abilities as a card counter and partly on the games you actually play in. I hope this article will help you better understand some of the issues involved in blackjack system simulations and comparisons. ♠
For complete information on the Red Seven, Advanced Red Seven, Hi-Lo Lite and Zen card counting systems, see Arnold Snyder's Blackbelt in Blackjack.Blackbelt also contains introductions to shuffle tracking, hole-card play, team play, and other advanced professional gambling techniques.
How To Find True Count In Blackjack Games
For complete information on the KO card counting system, see Knock-Out Blackjack by Olaf Vancura and Ken Fuchs.
Return to the Professional Gambling Library
Return to Blackjack Forum Online Home